L'indice di Sharpe e la teoria statistica asintotica per l'analisi di portafoglio
L’indice di Sharpe è dato dalla differenza tra il valore atteso di un portafoglio e il tasso risk free rapportato alla rischiosità del portafoglio rappresentata dalla deviazione standard. Esso rappresenta la maggior remunerazione richiesta dal risparmiatore per unità di rischio, e può essere ragionevolmente usato per valutare la bontà nelle scelte di composizione di portafoglio. La sua formulazione è la seguente:
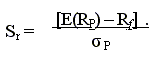
Tale formulazione è quella adottata per il CAPM ed è basata sull’ipotesi che la distribuzione dei rendimenti segua una distribuzione normale. Tale formulazione non è adatta ai fondi speculativi in quanto, come visto nel paragrafo 2, la distribuzione dei rendimenti dei fondi speculativi non è normale ma è asimmetrica verso sinistra e leptocurtica. Quindi la rischiosità di tali fondi deve essere modificata per includere queste caratteristiche.
B. Lee e Y. Lee hanno condotto una serie di studi, basati sulle simulazioni montecarlo, e altre approssimazioni analitiche e hanno trovato che molte di queste richiedevano alcune conoscenze sulla forma funzionale della funzione di rendimento che non erano disponibili nemmeno ai gestori. Di conseguenza essi hanno ripiegato sull’espansione di Cornish-Fisher.
Tale espansione modifica il quantile zα relativo all’intervallo di confidenza (1-α) relativo alla distribuzione normale, per tener conto dell’asimmetria e della curtosi.
La formulazione è la seguente:
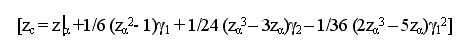
dove zc è il quantile di Cornish-Fisher e γ1 e γ2 sono i coefficienti che misurano l’asimmetria e la curtosi così come definiti nel paragrafo 2.
Una volta trovata la quantità zc la formulazione del rischio di portafoglio deve essere modificata passando da 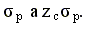
Nel 2002 Lo ha presentato uno studio, che basandosi sulla teoria statistica asintotica, e, applicando il teorema limite centrale, tentava di analizzare la condotta asintotica dell’indice di Sharpe.
Denotando con E(Ri) il rendimento atteso dell’i-esimo fondo e con σi la deviazione standard dell’i-esimo fondo e con Rit il rendimento conseguito dal fondo nel periodo (t-1, t) e ponendo E(Ri) = μi è possibile scrivere l’indice di Sharpe nel modo seguente:
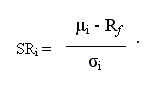
μ e σ2 rappresentano i momenti della distribuzione della popolazione e possono essere stimati sulla base di un campione con il metodo della massima verosimiglianza. In particolare la stima di μ e σ 2 è data rispettivamente da:
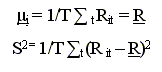
Dove R e S2 rappresentano gli stimatori, variabili casuali funzione del campione che si va ad esaminare, e T rappresenta il numero di osservazioni per ogni fondo. Definiti gli stimatori di media e varianza lo stimatore dell’indice di Sharpe è dato da:
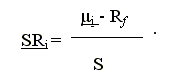
Usando la teoria statistica asintotica, con la quale è possibile applicare il teorema limite centrale, agli stimatori di μ e σ2 è possibile trovare la distribuzione asintotica di SR nell’ipotesi che Rt sia indipendente e identicamente distribuito (iid).
Sotto l’assunzione che i ritorni degli hedge funds siano iid e che presentino media e varianza finite gli stimatori μ e S2 presentano una distribuzione asintoticamente normale dovuta al teorema limite centrale.
Specificamente per ogni hedge funds abbiamo:
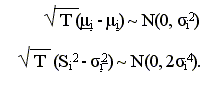
In tale modello la varianza degli stimatori tende a zero all’aumentare del campione, riflettendo come gli errori di stima si riducono all’aumentare della grandezza del campione.
Una volta trovati gli stimatori di media e varianza si può trovare lo stimatore dell’indice di Sharpe come funzione degli stimatori di media e varianza, come segue:
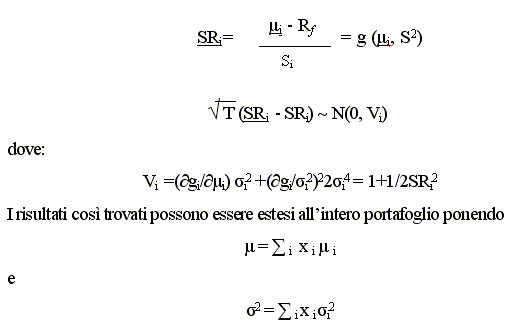
(si assume che la varianza del portafoglio sia la media ponderata delle varianze del portafoglio con covarianze nulle in quanto rendimenti e rischi dei diversi fondi sono in correlati).
In pratica assumere che il rendimento e il rischio dei diversi fondi siano indipendentemente ed identicamente distribuiti (zero correlation) è un’ipotesi irrealistica, pertanto il modello deve essere integrato per tener conto della non indipendenza e non identica distribuzione esistente tra gli hedge funds return.
Definiamo con X il vettore dei pesi, cioè X = (x1, x2, .......,xn) e con ξ il vettore delle medie e con ∑ la matrice varianza covarianza.
Il rendimento di n fondi in un periodo di tempo 0

di Domenico Aversano [Visita la sua tesi »] [Leggi i suoi articoli »]
 Iscriviti alla Newsletter Economia!
Iscriviti alla Newsletter Economia!
La redazione è online su Skype dalle 9 alle 13.
Contatta la nostra redazione a: [email protected] o via Skype